けろりんの数学ブログ

けろりんが数学のことをアウトプットするブログです

万年筆入門

はじめに

みなさんこんにちは,けろりんです.今回は私がいつも使っている"万年筆"についての記事です.この記事は"万年筆に興味はあるけれど,買うには至っていない"という方を沼へ引きずり込むへ向けた記事となっております.

万年筆に対する心理的障壁

まず,万年筆のイメージを見ていきましょう.

  • 高価
  • メンテナンスが面倒そう
  • 種類がありすぎてなにを買えばいいか分からない

あたりでしょうか.確かに高価なものは1本数万円するものもあります,またそのようなものはある程度大切に扱いたくなるものです.しかし,すべてがそのようなわけではありません.こんな悩みを全て解決してくれる1本を今回紹介させていただきます.

とりあえずこれ買っとけば間違いない

今回ご紹介させていただくのがこちらです.

プラチナ万年筆 万年筆 プレピー 0.2mm ブラック PSQ-400#1

プラチナ万年筆 万年筆 プレピー 0.2mm ブラック PSQ-400#1

プラチナ万年筆さんのpreppyという商品です.お値段なんと400円！知ってるか！preppy1本分のお金でpreppyが1本買えるんだぜ！
ということで激安万年筆です.色展開も豊富です.私は4本持っています.ちょっと前までは200円で売っていたのですが,値上がりしちゃいました.preppy1本分のお金で前はpreppyが2本買えたことになります.
さてこのpreppyなのですが,そのお値段のほかにもう一つ特徴があります.それが"スリップシール機構"というものなのですが,なんと1年放置しても大丈夫というものなんです.多少メンテナンスしなくてもなんの問題もありません.ひとまず買って遊んでみるのも手ではないでしょうか.
ということで私が万年筆の入門におすすめする1本はプラチナ万年筆のpreppyでした.公式サイトは プラチナ万年筆/プレピー です.色の展開,"スリップシール機構"の詳しい説明などが載っています.

合わせて買いたいもの

ここからは万年筆による遊び要素の紹介です.万年筆は万年筆だけで筆記ができるわけではなく,インクが必要です.インクから万年筆に興味を持たれる方も多いのではないでしょうか.インクを万年筆に供給する方法は2つあります.それが"カートリッジ"と"コンバータ"です.
"カートリッジ"は画像のようなカートリッジインクをそのまま万年筆にさすというもの.f:id:kukero:20180824234235j:plain "コンバータ"は画像にあるコンバータ(右下のものです)にインクを入れ,万年筆にさすというもの.f:id:kukero:20180824234440j:plain それぞれに良いところがあり,目的に応じて使い分ける必要があります.
まず"カートリッジ"ですが,インクの補充が簡単です.古いカートリッジを引っこ抜いて新しいモノをぶっさすだけです.また,万年筆を購入すると1つ付いてきます.ですので,本当に"万年筆を体験したい"というだけでしたらとりあえずこれだけ買っておけばよいでしょう.買い足す場合はこちらのようなものを買えばよいです.

プラチナ万年筆 万年筆カートリッジインク ブラック 10本 SPSQ-400#1

プラチナ万年筆 万年筆カートリッジインク ブラック 10本 SPSQ-400#1

カートリッジのだめなところは,(当然といえば当然ですが)カートリッジとして売られている色しか使えないという点です.世にはカートリッジとしては売られていない色のインクが星の数ほどあります.それを使うのに必要なのが"コンバータ"です.

プラチナ万年筆 万年筆インク吸入器 コンバーター コンバーター-500#0

プラチナ万年筆 万年筆インク吸入器 コンバーター コンバーター-500#0

こんなインクを使いたい！というものがある方には必須アイテムです.使い方などについてはここでは割愛させていただきます.
まとめると,インクに興味がある→インク+コンバータ,とりあえず万年筆を使いたい→必要になったときに替えのカートリッジを買えば問題無いと思われます.

おわりに

以上,万年筆入門でした.なにか質問がございましたらお気軽にコメントをよろしくお願いいたします.少しでも"万年筆はむずかしくない"ということが伝わったのであれば幸いです.最後までお読みいただきありがとうございました.

圏論から漂う"強キャラ"感

はじめに

みなさんこんにちは,けろりんです.最近(可換環論もろくにやらないまま)「圏論の技法」を買ってちょっとだけ読んでみたのですが,"圏論半端ないって!"と感じるところがあったので記事にしてみたいと思います.なおまだプログラミング言語でいう"Hello World"にあたるようなところしか読んでいませんので,大半が私の感想になります.

圏の定義について

圏の定義を見てみましょう.

圏{\mathcal{C}}とは,以下のようなものをいう.
(1){\mathcal{C}} の対象と呼ばれるもの全体{\mathrm{Ob}(\mathcal{C})}が与えられている.
(2){\mathcal{C}}の任意の二つの対象{X,Y}の間に,{X}から{Y}への射の集合{\mathcal{C}(X,Y)}が与えられている.射は以下の二つの性質を満たす.
(i)二つの射が{X\xrightarrow{f} Y\xrightarrow{g}Z}のように続いている時,これらの合成{g\circ f\in\mathcal{C}(X,Z)}が与えられ,結合則を満たす.　　 (ii){\mathcal{C}}の任意の対象{X}に対して,恒等射と呼ばれる射{\mathrm{id}_X\in\mathcal{C}(X,X)}がひとつずつ与えられており,合成に対して単位元的にふるまう.

ｴ､ﾅﾆｺﾚｲﾐﾜｶﾝﾅｲ!?なんと対象に対して元を取る操作が許されていないのです.つまりある集合とその上の写像を圏とみなす場合,その集合がどういうものが集められたものなのか,ということは無視されてしまうのです.それって,魂を抜かれたも同然だろという気分になってしまいます.ですが,この"抽象 of the worldみ"が圏論の強そうなところでもあるのです.
この性質を考えると,前回の記事 準同型と普遍性 - けろりんの数学ブログにて散々分からないと嘆いていた"普遍性"についても若干の理解が得られるような気がします.
射と対象のみしか議論の対象とならない圏論においてある物事を定義しようとしたときに,射が対象についてどう振る舞うかを定めることでしか定義のしようがないのです.考える対象を固定して(可換環,群など)概念(積など)を定義するのではなくて,その概念そのものがどういうものなのかを定義してやろう,というのが圏論での定義,になるのかな,などと思いました.(めっちゃ強そう...)

おわりに

短い記事になってしまいましたね...最後までお読みいただきありがとうございました.

準同型と普遍性

ごあいさつ

みなさんこんにちは,けろりんです.
最初の記事 Cauchy列と収束列 - けろりんの数学ブログがたくさんの方にご覧いただけたようで,大変驚いています.ありがとうございます.
記事のほかに面白いことがあればぜひ教えていただけると嬉しいです.
さて,本日は"準同型と普遍性"というタイトルで記事を書いていくのですが,実は可換図式のTeX打ちの練習のための記事だったりします.

本題に入る前の注意なのですが,私はまだ"普遍性"について理解できておりません.ですので,本文中で間違った解釈を書いてしまっている点があるかもしれません.間違っている点,より良く解釈できそうな点などがございましたらご指摘いただけるとありがたいです.

準同型性の"お気持ち"

それでは本題に入りましょう.今回の舞台は可換環です.可換環{R},{R-}加群{M,N}が与えられたとします.このとき,存在する演算とは何でしょうか.もちろん{R}における和,積と{M,N}における和,{R}によるスカラー倍ですね.この時点では{M,N}は同じ{R-}加群という以外には全く関係の無いものです.さて,ここで加群の準同型{f:M\to N}が与えられたとします.これによって{M,N}の間には集合論的な写像という意味を超えた,"橋"が架けられたことになります(この時点では一方通行なものではありますが).
ここで加群における準同型性を確認しましょう.

(1){x,y\in M}に対し,{f(x+y)=f(x)+f(y)}
(2){r\in R,x\in M}に対し,{f(rx)=rf(x)}
以上が成立するとき{f:M\to N}を{R}上の加群準同型という

といったものでした.ここで注意したいのが演算の種類です.(1)の左辺の括弧内は{M}内の和,右辺は{N}内の和/(2)の左辺の括弧内は{R,M}のスカラー倍,右辺は{R,N}のスカラー倍です.写像{f}は集合の元だけでなく演算規則すらも結び付けてしまったことがお分かりいただけるでしょうか.
このように"セカイをつなぐ"ような性質を準同型性というのでした.

普遍性について

それでは普遍性について,に移りたいと思います.ここで普遍性による直積の定義,を例に取りたいと思います.以下が加群の直積の定義です.

{(M_\lambda)_{\lambda\in\Lambda}}を{R-}加群の族とする.このとき{(M_\lambda)}の直積とは加群{\prod_{\lambda\in\Lambda}}および,各{\lambda\in\Lambda}に対する準同型の族{p_\lambda:\prod M_\lambda\to M_\lambda}で,次の性質を満たすものである.

任意の{R-}加群{N}と各{\lambda\in\Lambda}に対する{R}上の加群準同型{q_\lambda:N\to M_\lambda}の族に対し,{R}上の加群準同型{f:N\to\prod M_\lambda}で{f\circ p_\lambda=q_\lambda},つまり次の図式が可換になるものが一意的に存在する

f:id:kukero:20180615004646j:plain

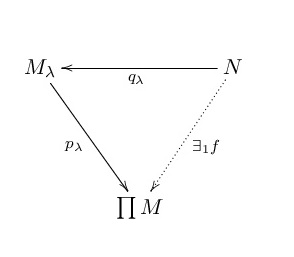
いかがでしょうか.*1これが普遍性による直積の定義です.
私の読んだ文書の中には,"構成の仕方よりも機能に注目し,その機能だけを抜き出したものを定義とするのが普遍性による定義です",という説明がありました.しかし私はその意味が全く理解できませんでした.つまり,"なぜそれを普遍性による定義というのか分からない"というような状態です.(というか今もその状態です)率直に言うと,構成しているのと違いが分からない,結局その"普遍性"というのは構成により得られたものではないか？,というのが思うところであります.仮に構成を経由することなく普遍性により定義したとき,それは本当に存在するのでしょうか,そしてそれを確認するにはもはや構成するしかないのではないでしょうか.
現在,圏論的に,つまり定義したいことに言及するのではなく,他との関わりによりそれを定義する(この解釈が合っているのかも圏論に詳しくないので分からないところではありますが)ためにこのような定義にしている,というような非常にもやもやとする解釈になってしまっています.以上が現時点での私の"普遍性"に対する解釈であります.
解釈/記述の間違っている点,記述の分かりにくい点,その他ご意見などございましたら,お手数ですがご指摘の方よろしくお願いいたします.

おわりに

解釈というより分からないを発信する記事になってしまい,まことに申し訳ございません.
最後までお読みいただきありがとうございました.

*1:可換図式書くの,思ったより簡単にできますね(時間は相当かかりましたが...)

Cauchy列と収束列

解析

はじめまして

はじめまして,けろりんです.
アウトプットの練習の場としてブログを始めさせていただきます.
数学の"お気持ち"を理解したい大学生です.最近の興味は力学系,可換環論などです.

Cauchy列と収束列

それでは本題に入ります.大学1回生の時の微分積分学の講義においてこんなことを習いました.
Cauchy列ならば収束列である.
これ,実は一般的には成り立たないんです.一般的に成り立つのは
収束列ならばCauchy列である.
だけなんです.それではまずは2つの定義から見ていきましょう.

数列{ {a_n}_{(n\in\mathbb{N})} }が以下を満たすときCauchy列であるという.*1
{\displaystyle {}^\forall\varepsilon\gt0,{}^\exists N\in\mathbb{N},\mathrm{s.t.}"m,n\geq N \Rightarrow |a_n - a_m|\lt\varepsilon }

数列{ {a_n}_{(n\in\mathbb{N})} }が以下を満たすとき数列は{\alpha}に収束するといい,この数列は収束列であるという.
{\displaystyle {}^\forall\varepsilon\gt0,{}^\exists N\in\mathbb{N},\mathrm{s.t.}"n\geq N \Rightarrow |a_n - \alpha|\lt\varepsilon }

おなじみの定義ですね.では収束列ならばCauchy列を(ほぼ明らかではありますが)示していきたいと思います.

収束列{\Rightarrow}Cauchy列

収束列ということで {\displaystyle {}^\forall\varepsilon\gt0,{}^\exists N\in\mathbb{N},\mathrm{s.t.}"n\geq N \Rightarrow |a_n - \alpha|\lt\varepsilon }
が成立します.この{N}に対して{n,m\gt N}となるような{n,m}を任意に取ると
{\displaystyle |a_n-a_m|=|a_n-\alpha-(a_m-\alpha)|\leq |a_n-\alpha|+|a_m-\alpha|\lt 2\varepsilon }
が成立,これは数列がCauchy列になっていることを示しています.

Cauchy列{\Rightarrow}収束列

これは一般には成り立たないと言いましたが,その違いを表すキーワードが完備性です.完備性を持つ空間上の数列についてはCauchy列{\Rightarrow}収束列が成立します.もちろん実数は完備性を持ちます.微分積分学のはじめの講義でDedekindの公理,Cantorの区間縮小法,Weierstrassの定理などをやりますが,これらは全て実数に完備性*2を公理的に与える作業だったのです.(実数というのは完備性を持つもの,というのを前提にしてこれから議論を進めますよ～～,という意味です.)
つまりこれが成り立たない例を見るには,完備性を無くしてやればいいのです.ということで少しだけ"セカイを狭めて"やりましょう.これからは有理数上の数列を考えることにします.

有理数上の数列{{a_n}}について各々の項を以下のように定めることにします.
{a_0=1}
{a_1=1.4}
{a_2=1.41}
{a_3=1.414}
{a_4=1.4142}
{\vdots}

これらの数列の各項は有理数の値を取ります.お察しの通りこの数列は{\sqrt{2}}に収束する……と言いたいところなのですが,今の"セカイ"は有理数,{\sqrt{2}}なんて数は知らないわけです.収束の定義のところに明示はしていなかったのですが,数列の項と収束先のいる"セカイ"は一緒でなくてはなりません.ですので,この数列は"有理数の範囲内では"収束しないといえます.これがCauchy列であることはまあ明らかでしょうから,これで"Cauchy列ならば収束列"の反例を挙げることができました.*3

おわりに

完備 is 偉大,ということが伝わったのであれば幸いです.
解釈/記述の間違っている点,記述の分かりにくい点,その他ご意見などございましたら,お手数ですがご指摘の方よろしくお願いいたします.
最後までお読みいただきありがとうございました.

*1:{a_n}にちゃんと{}つけてるはずなのについてないのは何故…？\{\}ではないの…？有識者氏～～

*2:稠密性と混同している方をよくお見掛けしますが,異なる概念ですので注意してください.

*3:収束先を"くっつける"ことで"セカイ"を拡張する,という事もできます.これを完備化といいます.