ごあいさつ

みなさんこんにちは,けろりんです.
最初の記事 Cauchy列と収束列 - けろりんの数学ブログがたくさんの方にご覧いただけたようで,大変驚いています.ありがとうございます.
記事のほかに面白いことがあればぜひ教えていただけると嬉しいです.
さて,本日は"準同型と普遍性"というタイトルで記事を書いていくのですが,実は可換図式のTeX打ちの練習のための記事だったりします.

本題に入る前の注意なのですが,私はまだ"普遍性"について理解できておりません.ですので,本文中で間違った解釈を書いてしまっている点があるかもしれません.間違っている点,より良く解釈できそうな点などがございましたらご指摘いただけるとありがたいです.

準同型性の"お気持ち"

それでは本題に入りましょう.今回の舞台は可換環です.可換環 ${R}$ , ${R-}$ 加群 ${M,N}$ が与えられたとします.このとき,存在する演算とは何でしょうか.もちろん ${R}$ における和,積と ${M,N}$ における和, ${R}$ によるスカラー倍ですね.この時点では ${M,N}$ は同じ ${R-}$ 加群という以外には全く関係の無いものです.さて,ここで加群の準同型 ${f:M\to N}$ が与えられたとします.これによって ${M,N}$ の間には集合論的な写像という意味を超えた,"橋"が架けられたことになります(この時点では一方通行なものではありますが).
ここで加群における準同型性を確認しましょう.

(1) ${x,y\in M}$ に対し, ${f(x+y)=f(x)+f(y)}$
(2) ${r\in R,x\in M}$ に対し, ${f(rx)=rf(x)}$
以上が成立するとき ${f:M\to N}$ を ${R}$ 上の加群準同型という

といったものでした.ここで注意したいのが演算の種類です.(1)の左辺の括弧内は ${M}$ 内の和,右辺は ${N}$ 内の和/(2)の左辺の括弧内は ${R,M}$ のスカラー倍,右辺は ${R,N}$ のスカラー倍です.写像 ${f}$ は集合の元だけでなく演算規則すらも結び付けてしまったことがお分かりいただけるでしょうか.
このように"セカイをつなぐ"ような性質を準同型性というのでした.

普遍性について

それでは普遍性について,に移りたいと思います.ここで普遍性による直積の定義,を例に取りたいと思います.以下が加群の直積の定義です.

を加群の族とする.このときの直積とは加群および,各に対する準同型の族で,次の性質を満たすものである.

任意の加群と各に対する上の加群準同型の族に対し,上の加群準同型で,つまり次の図式が可換になるものが一意的に存在する

f:id:kukero:20180615004646j:plain

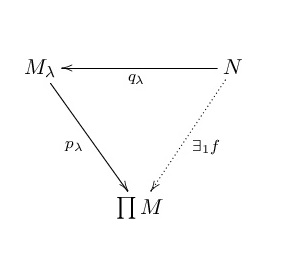
いかがでしょうか.*1これが普遍性による直積の定義です.
私の読んだ文書の中には,"構成の仕方よりも機能に注目し,その機能だけを抜き出したものを定義とするのが普遍性による定義です",という説明がありました.しかし私はその意味が全く理解できませんでした.つまり,"なぜそれを普遍性による定義というのか分からない"というような状態です.(というか今もその状態です)率直に言うと,構成しているのと違いが分からない,結局その"普遍性"というのは構成により得られたものではないか？,というのが思うところであります.仮に構成を経由することなく普遍性により定義したとき,それは本当に存在するのでしょうか,そしてそれを確認するにはもはや構成するしかないのではないでしょうか.
現在,圏論的に,つまり定義したいことに言及するのではなく,他との関わりによりそれを定義する(この解釈が合っているのかも圏論に詳しくないので分からないところではありますが)ためにこのような定義にしている,というような非常にもやもやとする解釈になってしまっています.以上が現時点での私の"普遍性"に対する解釈であります.
解釈/記述の間違っている点,記述の分かりにくい点,その他ご意見などございましたら,お手数ですがご指摘の方よろしくお願いいたします.

おわりに

解釈というより分からないを発信する記事になってしまい,まことに申し訳ございません.
最後までお読みいただきありがとうございました.

*1:可換図式書くの,思ったより簡単にできますね(時間は相当かかりましたが...)